Solution of Lti System State Space Representation Oscillator
 |  |  |  | |
|---|
A step response is a common evaluation of the dynamics of a simulated system. A linear time invariant (LTI) system can be described equivalently as a transfer function, a state space model, or solved numerically with and ODE integrator. This tutorial shows how to simulate a first and second order system in Python.
First Order System Simulation
Consider a first order differential equation with constants `K_p=3` and `\tau_p=2`, input `u`, and output response `y`.
$$\tau_p \frac{dy}{dt} = -y + K_p u$$
Three methods to represent this differential equation is as a (1) transfer function, (2) state space model, and (3) semi-explicit differential equation. Source code is included below to simulate a step response in these three forms.
1. Transfer Function
$$\frac{Y(s)}{U(s)} = \frac{K_p}{\tau_p \,s + 1}$$
2. State Space Model
$$\dot x = A x + B u$$
$$y = C x + D u$$
$$A = -\frac{1}{\tau_p} \quad B = \frac{K_p}{\tau_p} \quad C=1 \quad D=0$$
3. Differential Equation
$$\frac{dy}{dt} = -\frac{1}{\tau_p} y + \frac{K_p}{\tau_p} u$$
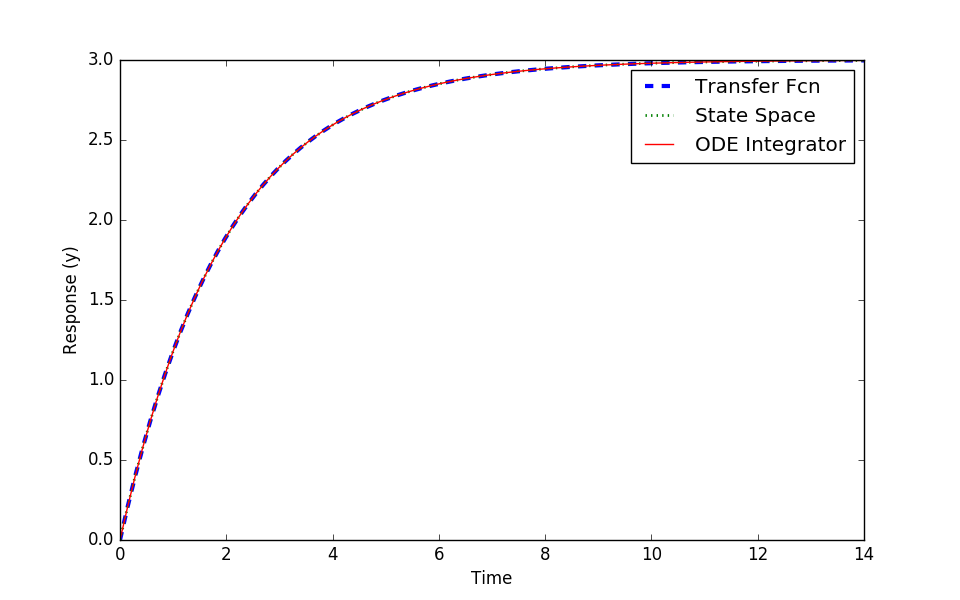
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# Simulate taup * dy/dt = -y + K*u
Kp = 3.0
taup = 2.0
# (1) Transfer Function
num = [Kp]
den = [taup, 1 ]
sys1 = signal.TransferFunction (num,den)
t1,y1 = signal.step (sys1)
# (2) State Space
A = -1.0/taup
B = Kp/taup
C = 1.0
D = 0.0
sys2 = signal.StateSpace (A,B,C,D)
t2,y2 = signal.step (sys2)
# (3) ODE Integrator
def model3(y,t):
u = 1
return (-y + Kp * u)/taup
t3 = np.linspace ( 0 , 14 , 100 )
y3 = odeint(model3, 0 ,t3)
plt.figure ( 1 )
plt.plot (t1,y1, 'b--' ,linewidth= 3 ,label= 'Transfer Fcn' )
plt.plot (t2,y2, 'g:' ,linewidth= 2 ,label= 'State Space' )
plt.plot (t3,y3, 'r-' ,linewidth= 1 ,label= 'ODE Integrator' )
plt.xlabel ( 'Time' )
plt.ylabel ( 'Response (y)' )
plt.legend (loc= 'best' )
plt.show ( )
Second Order System Simulation
1. Laplace Domain, Transfer Function
$$\frac{Y(s)}{U(s)} = \frac{K_p}{\tau_s^2 s^2 + 2 \zeta \tau_s s + 1}e^{-\theta_p s}$$
2. State Space Form
$$\begin{bmatrix}\dot x_1\\\dot x_2\end{bmatrix} = \begin{bmatrix}0&1\\-\frac{1}{\tau_s^2}&-\frac{2 \zeta}{\tau_s}\end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} + \begin{bmatrix}0\\\frac{K_p}{\tau_{s}^2}\end{bmatrix} u\left(t-\theta_p\right)$$
$$y = \begin{bmatrix}1 & 0\end{bmatrix} \begin{bmatrix}x_1\\x_2\end{bmatrix} + \begin{bmatrix}0\end{bmatrix} u$$
3. Second Order Differential Equation
$$\tau_s^2 \frac{d^2y}{dt^2} + 2 \zeta \tau_s \frac{dy}{dt} + y = K_p \, u\left(t-\theta_p \right)$$

Kp = 2.0 # gain tau = 1.0 # time constant zeta = 0.25 # damping factor theta = 0.0 # no time delay
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# tau * dy2/dt2 + 2*zeta*tau*dy/dt + y = Kp*u
Kp = 2.0# gain
tau = 1.0 # time constant
zeta = 0.25 # damping factor
theta = 0.0 # no time delay
du = 1.0# change in u
# (1) Transfer Function
num = [Kp]
den = [tau**2 , 2*zeta*tau, 1 ]
sys1 = signal.TransferFunction (num,den)
t1,y1 = signal.step (sys1)
# (2) State Space
A = [ [ 0.0 , 1.0 ] , [-1.0/tau**2 ,-2.0*zeta/tau] ]
B = [ [ 0.0 ] , [Kp/tau**2 ] ]
C = [ 1.0 , 0.0 ]
D = 0.0
sys2 = signal.StateSpace (A,B,C,D)
t2,y2 = signal.step (sys2)
# (3) ODE Integrator
def model3(x,t):
y = x[ 0 ]
dydt = x[ 1 ]
dy2dt2 = (-2.0*zeta*tau*dydt - y + Kp*du)/tau**2
return [dydt,dy2dt2]
t3 = np.linspace ( 0 , 25 , 100 )
x3 = odeint(model3, [ 0 , 0 ] ,t3)
y3 = x3[:, 0 ]
plt.figure ( 1 )
plt.plot (t1,y1*du, 'b--' ,linewidth= 3 ,label= 'Transfer Fcn' )
plt.plot (t2,y2*du, 'g:' ,linewidth= 2 ,label= 'State Space' )
plt.plot (t3,y3, 'r-' ,linewidth= 1 ,label= 'ODE Integrator' )
y_ss = Kp * du
plt.plot ( [ 0 , max (t1) ] , [y_ss,y_ss] , 'k:' )
plt.xlim ( [ 0 , max (t1) ] )
plt.xlabel ( 'Time' )
plt.ylabel ( 'Response (y)' )
plt.legend (loc= 'best' )
plt.savefig ( '2nd_order.png' )
plt.show ( )
Higher Order Simulation
A simple higher order simulation is the combination of n first order equations. The value of the time constant is 10/n in this example. The first equation is a first order differential expression.
$$\tau \frac{dy_1}{dt} = -y_1 + 1$$
Additional equations are also first order differential expressions for i = 2, n.
$$\tau \frac{dy_i}{dt} = -y_i + y_{i-1}$$
Solution of Lti System State Space Representation Oscillator
Source: https://apmonitor.com/pdc/index.php/Main/ModelSimulation